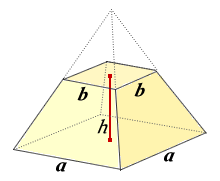
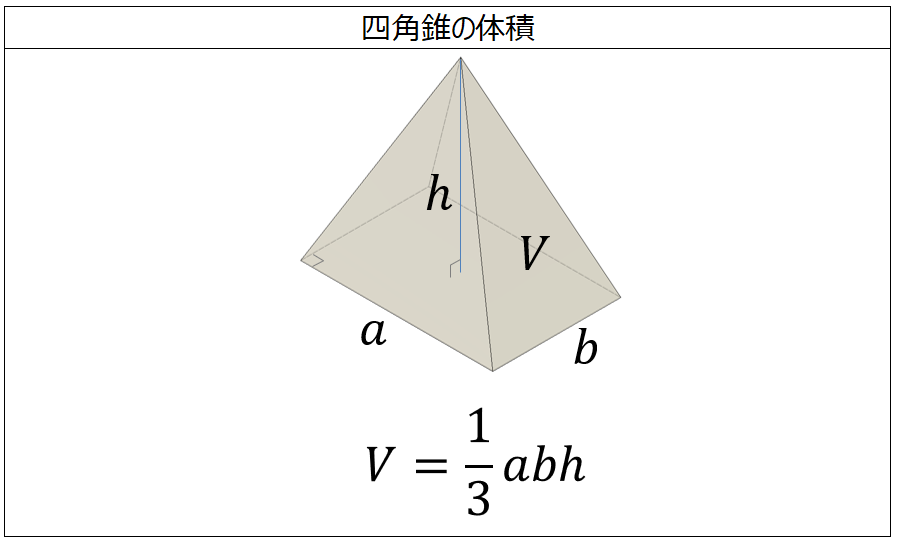
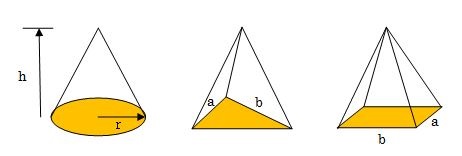
正四角錐(せいしかくすい) 高さを h としたとき、底面積 A は自明なことに A = ab、体積 V は錐体の体積の公式から V = Ah / 3 = abh / 3 で与えられる。直錐の場合、側面積 S は = となる。 任意の正四角錐は、適当なAcは底面の正方形abcdの対角線なので ≫ 三平方の定理に当てはめて ac 2 =12 2 12 2 ac 2 =2 ac=±12 2 ac>0より ac=12 2 oからacに引いた垂線をomとすると これが四角錐の高さになる。 amはacの 1 2 なので am=6 2 ≫ o a c 15cm 15cm m 12 2 cm 6 2 cm oamで三平方の定理を使うと 15 2 =om正四角錐bdegの体積は,立方体abcdefghから,合同な4つの四角錐の体積を引くことで求められる。aを用いて,立方体abcdefghの体積は, ア cm3と表せ,四角錐abceの体積は, イ cm3と表せる。
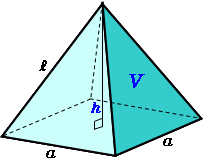
正四角錐の体積 底辺と側辺から 高精度計算サイト
正四 角錐 の 体積
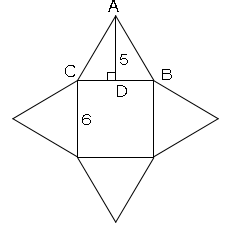
正四 角錐 の 体積-で、左の正四角錐はこれを6で割ったものですので、正四角錐の体積は\(\frac{ 4 }{ 3 }h^3\)になりますね。 ということは、正四面体の体積は底面と高さの積を何倍すればいいのでしょう? (?倍すればいいと考えます) 底面は一辺\(2h\)の正方形、高さは\(h\)ですの正四角錐の体積の問題になります。 基本的な問題なのでできるようにしておきましょう。 問題6 図は1辺が6cmの正方形の周りに、それぞれの辺を底辺とし、高さが5cmの二等辺三角形を四枚並べてみたものである。



空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
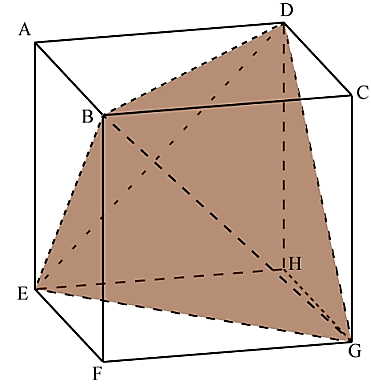
正四角錐bdegの体積は,立方体abcdefghから,合同な4つの四角錐の体積を引くことで求められる。aを用いて,立方体abcdefghの体積は, ア cm3と表せ,四角錐abceの体積は, イ cm3と表せる。体積=6 2 ×π×3√5÷3=36√5π(㎤) 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺の1辺が6cm 他の辺が9cmの四角すいの体積を考える 直角三角形OAHから三平方の定理を利用して高さOHを求めればよい。 まずAHの長さを求めるある体積V 1を 有する三角正四角錐があると仮定する。 それに相似なピラミッドを最初のものよりも3倍小さい体積にするためには、この図のサイズを何倍に縮小すればよいでしょうか。 元の正角錐の公式を書くことによって、問題を解決し始めます。
計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを 高中 B4 1 1 兩面角 四角錐 尹正數學 Youtube四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。
正四角錐の体積の問題になります。 基本的な問題なのでできるようにしておきましょう。 問題6 図は1辺が6cmの正方形の周りに、それぞれの辺を底辺とし、高さが5cmの二等辺三角形を四枚並べてみたものである。体積の利用 \(ce\) の長さは、底面を三角形 \(oab\) と見たときの 三角錐の髙さになっています。 つまり「体積」から計算できます。 その1で、「(1)この正三角錐の体積を求めなさい。」 を解説しております。 体積は \(6cm^3\) です。 底面が \(oab\) 高さを \(ce\)四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式


塾 学校 家庭を結ぶ 受験情報サイト 学びネット
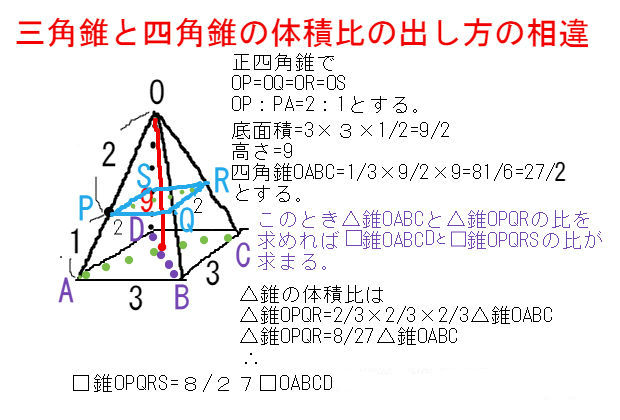


三角錐と四角錐の体積比計算方法の違い 中学数学 理科 寺子屋塾の復習サイト
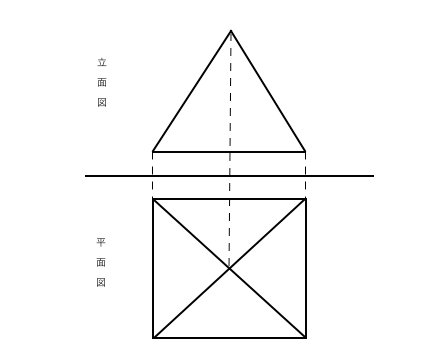
で、左の正四角錐はこれを6で割ったものですので、正四角錐の体積は\(\frac{ 4 }{ 3 }h^3\)になりますね。 ということは、正四面体の体積は底面と高さの積を何倍すればいいのでしょう? (?倍すればいいと考えます) 底面は一辺\(2h\)の正方形、高さは\(h\)ですの四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式中3 数学 右の図3は正四角錐の投影図ですこの四角錐の 立面図は1辺の長さが6 cm の正三角形ですこの正四角錐の体積を求めなさい この問題がなぜかどうしても解けません。 こたえは36√3立方センチメートルです



壮大 台形 体積 求め 方 壁紙 配布



高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ
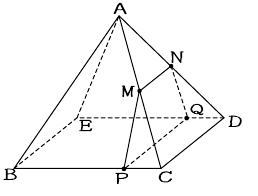
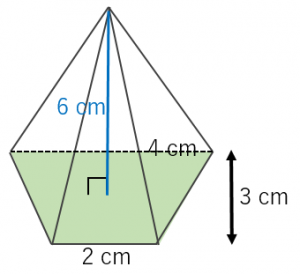
数学を解く楽しさを伝えたい 数が苦→数楽に!! チャンネル登録はこちら ︎ https//bitly/39v2H5B / Twitterはこちら https//twitter正四角錐bdegの体積は,立方体abcdefghから,合同な4つの四角錐の体積を引くことで求められる。aを用いて,立方体abcdefghの体積は, ア cm3と表せ,四角錐abceの体積は, イ cm3と表せる。すべての辺の長さが2 cm である正四角錐oabcd において,辺oc 上に中点e をとる。この正四角錐の 側面上に,頂点a から辺ob と交わり点e まで線をひ くとき,最も短くなるようにひいた線の長さを求めな さい。 類題 2 1 辺が6cm の正方形abcd について,辺bc


正四角錐の体積の問題 数学の要点まとめ 練習問題一覧
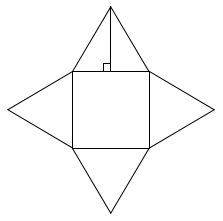


正四角錐の体積の問題 数学の要点まとめ 練習問題一覧
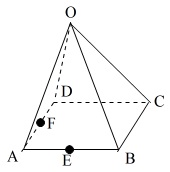
直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の数学を解く楽しさを伝えたい 数が苦→数楽に!! チャンネル登録はこちら ︎ https//bitly/39v2H5B / Twitterはこちら https//twitter正四角錐oabcdにおいて、底面は1辺の長さが4の正方形で、側面は1辺の長さが4の正三角形である。 ①正四角錐oabcdの体積を求めよ。 ②辺oa,ob上にそれぞれoppa=31, oqqb=31をみたす点p,qをとる。このとき、五
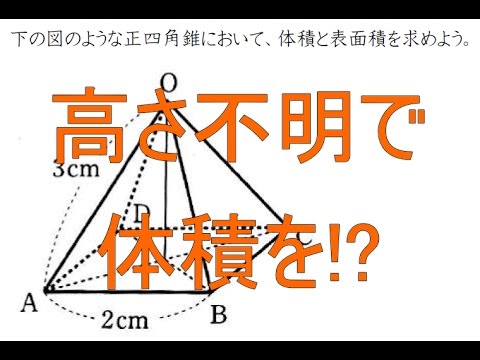


正四角錐と三平方の定理 中学3年数学 Youtube


13年12月29日 四角錐の体積はなぜ四角柱の1 3なのか いつかきっと辿り着くまで
底面がひし形で obdが正三角形の四角錐の体積を求めなさい。という問題の解き方を教えてください!情報などは下の図に書きました。分かりにくい図かもしれないのですが解説よろしくお願いし ます! ひし形は4辺直方体の体積 四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の正四角錐の体積 = 64×7÷3 = 448 3 cm 3 つぎの立体のの体積を求めよ。 母線の長さ 13cm, 底面の半径5cmの円錐 母線の長さ 6cm, 底面の半径4cmの円錐 母線の長さ 7cm, 底面の半径2cmの円錐 底面が1辺12cmの正方形で、他の辺が11cmの正四角錐 底面が1辺4cmの正方形で、他の


Studydoctor正四角錐と三平方の定理 中学3年数学 Studydoctor
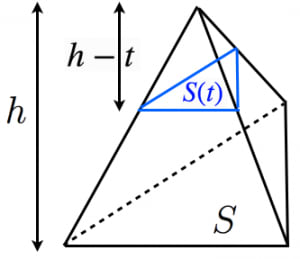


錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語
正四角錐の体積 = 64×7÷3 = 448 3 cm 3 つぎの立体のの体積を求めよ。 母線の長さ 13cm, 底面の半径5cmの円錐 母線の長さ 6cm, 底面の半径4cmの円錐 母線の長さ 7cm, 底面の半径2cmの円錐 底面が1辺12cmの正方形で、他の辺が11cmの正四角錐 底面が1辺4cmの正方形で、他の


Math 立体の切断 高校入試に出る難しい問題 働きアリ The 2nd



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
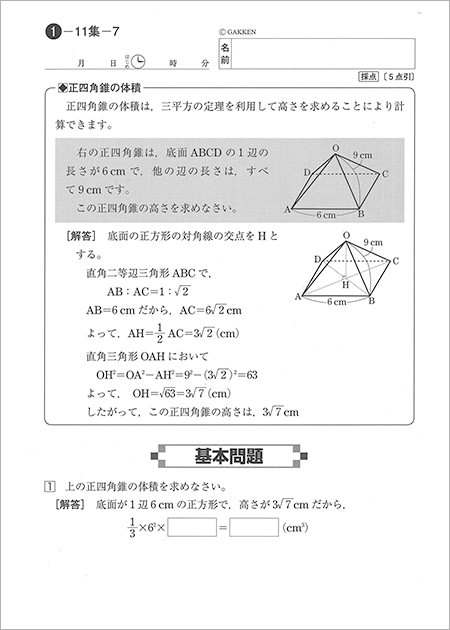


学研教室



円錐は1 3 中学生に分かるように真剣に考えてみた うちーノート



なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4



四角錐の表面積の求め方 公式 小学生 中学生の勉強



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成
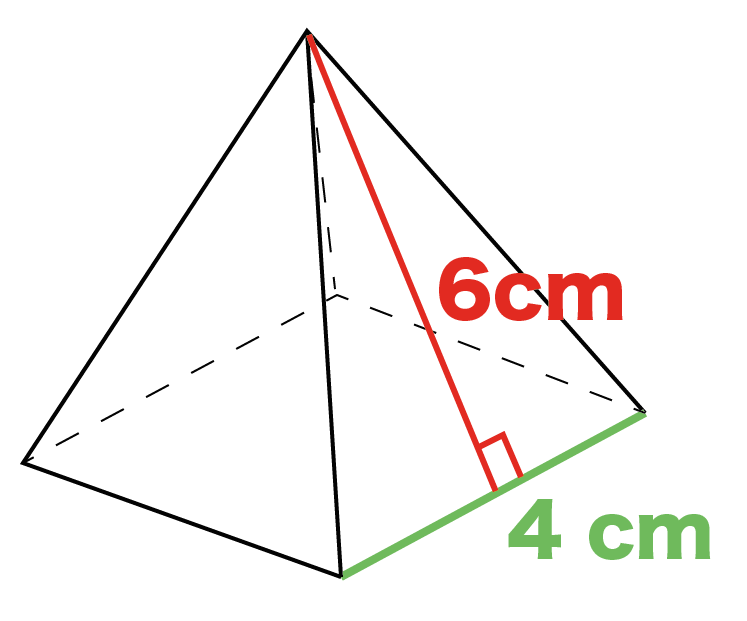


簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく


三平方の定理8 解説


立体の体積 空間図形 中学1年 数学クラブ



四角錐台の体積 高精度計算サイト



空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
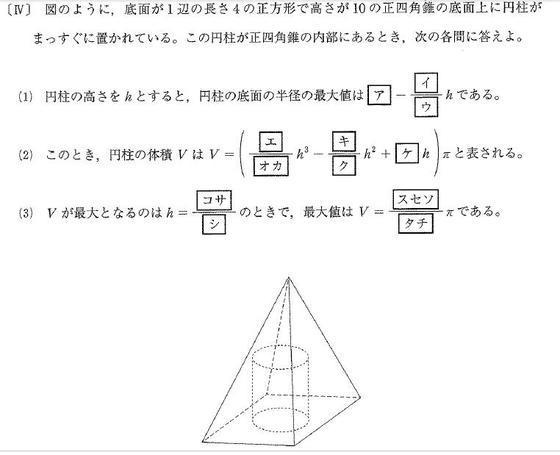


正四角錐に内接する円柱の体積の最大問題です 大学入試数学問題の解説 解答



4862 体積 四角錐の断面 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱



正四角錐の表面積と体積の求め方を教えてください Clear



四角錐の体積比の公式は がんばりすぎない 改め がんばる中学受験 その後



角錐 円錐の体積と表面積の公式 数学fun


第360問の解答



角錐 円錐の体積 Youtube



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


正四角錐の体積と比率 高校入試 数学 良問 難問


円錐 すい の表面積や四角錐 五角錐の体積の求め方


四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア
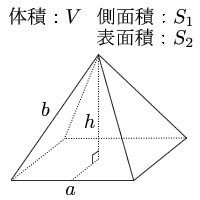


正四角錐 底辺と高さ 体積 表面積の計算 計算サイト



三平方の定理の利用 四角錐 円錐 チーム エン


正4角錐の体積の式を紙工作で実証する 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ


四角錐の体積 中学から数学だいすき



正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



高校受験 中学数学 正四角錐と体積比 Youtube


四角錐に関する問題



角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学


正四角錐の体積と表面積と底面積の求め方を教えてくださいaが8cm Yahoo 知恵袋
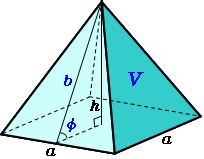


正四角錐の体積 底辺と高さから 高精度計算サイト


第87問の解答



直撃 中学入試 第135回 筑波大附属中 立体 正四角錐の切断 北辰塾 情報局


算数にチャレンジ にチャレンジ 11



四角錐の体積の求め方 公式 小学生 中学生の勉強



どうして1 3なの 錐の体積の公式の求め方 まなべーと
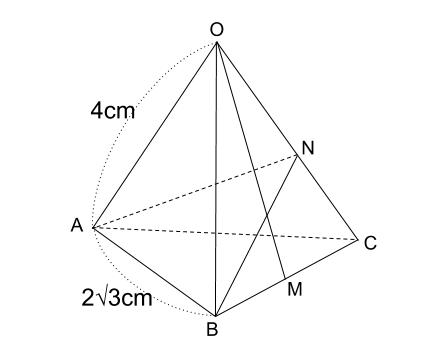


正四角錐の良問 その1 中学数学の無料オンライン学習サイトchu Su
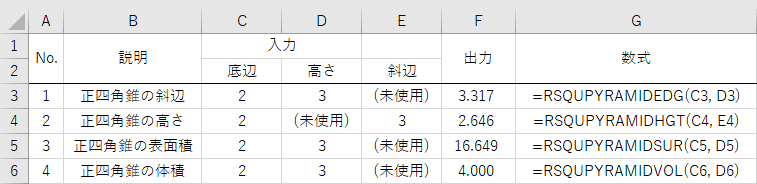


画像 正四 角錐 の 体積 Hd壁紙画像fhd



中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット


三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学


みんなの知識 ちょっと便利帳 正四角錐台の体積を計算する



最高正四 角錐 体積 ただぬりえ



56 四角錐の切断と体積 Youtube



体積の求め方 計算公式一覧



どうして1 3なの 錐の体積の公式の求め方 まなべーと


体積の計算 四角錐 製品設計知識



Ppt 四角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id 7703


超難問 正四角錐の切断面の面積と切断立体の体積 中学数学 理科 寺子屋塾の復習サイト



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく


毎日問題を解こう 11 苦手な数学を簡単に



立体の体積 無料で使える中学学習プリント


Math 角錐の体積が角柱の3分の1になる証明 働きアリ The 2nd



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
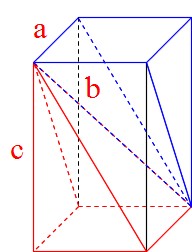


Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ



公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成


立体図形の体積


知恵袋に 正四角錐とそれに内接する球の体積比と面積比 アップ 久保塾 今治市の学習塾


第57問の解答



四角錐の展開図の切り出し 名古屋市立大学14年 理系のための備忘録
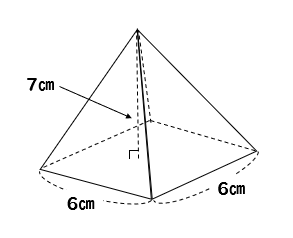


3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学


正四角錐の展開図が8通りあるそうなのですが ご存じの方どなたか Yahoo 知恵袋



正四角錐の問題 高校数学に関する質問 勉強質問サイト


四角錐の体積
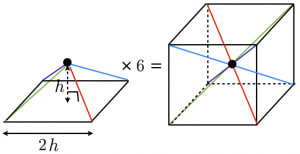


錐体の体積に1 3がつくことの2通りの説明 高校数学の美しい物語



四角錐 Wikipedia



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ


辺の長さが全て4である正四角錐がある P Qは中点である このと Yahoo 知恵袋
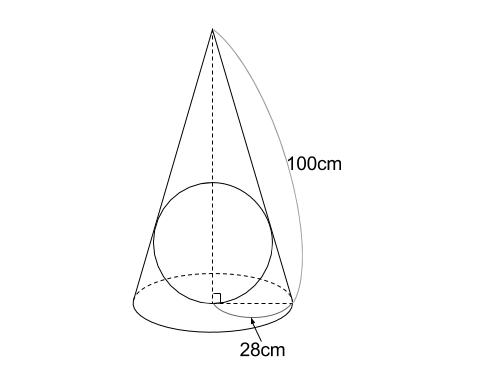


円錐と内接球 その1 中学数学の無料オンライン学習サイトchu Su


錐 すい の体積の計算 もう一度やり直しの算数 数学



角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun



四角錐 Wikipedia
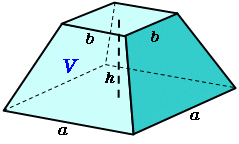


正四角錐台の体積 高精度計算サイト


四角錐 Wikipedia



台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学



正四角錐の体積 底辺と側辺から 高精度計算サイト
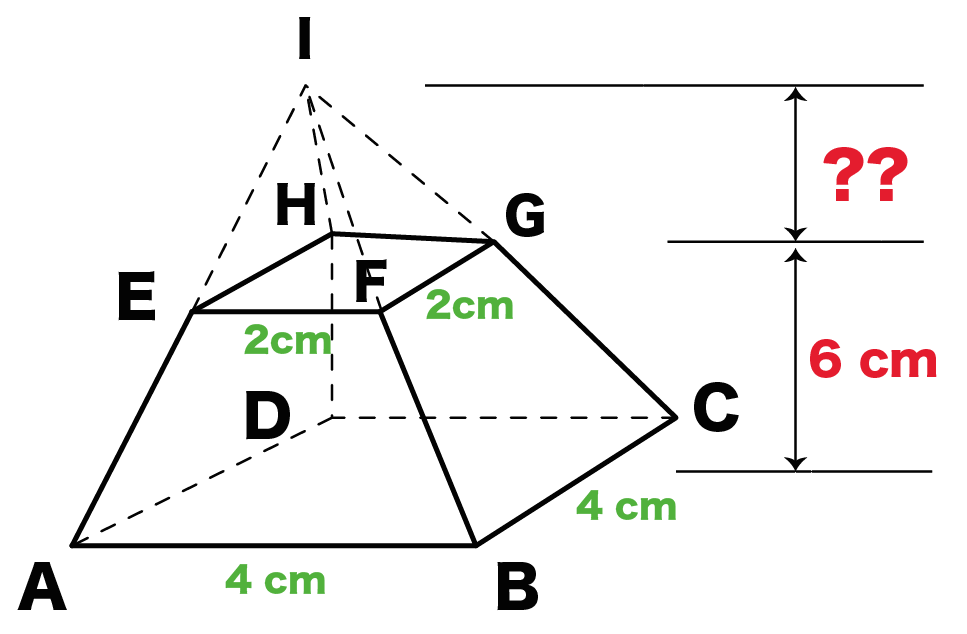


簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
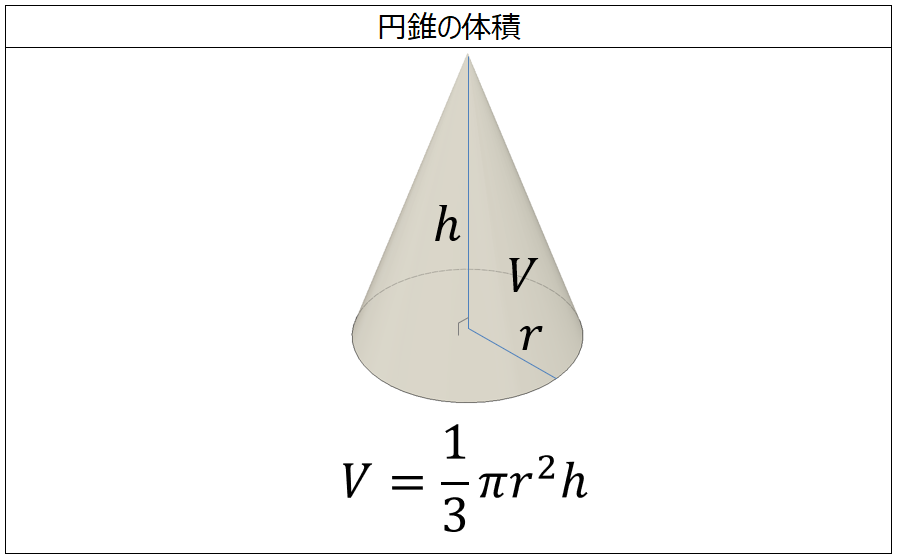


体積の計算 円錐 製品設計知識



体積について 図のように立方体の1つの面の各辺の中点と その面に平行 数学 教えて Goo
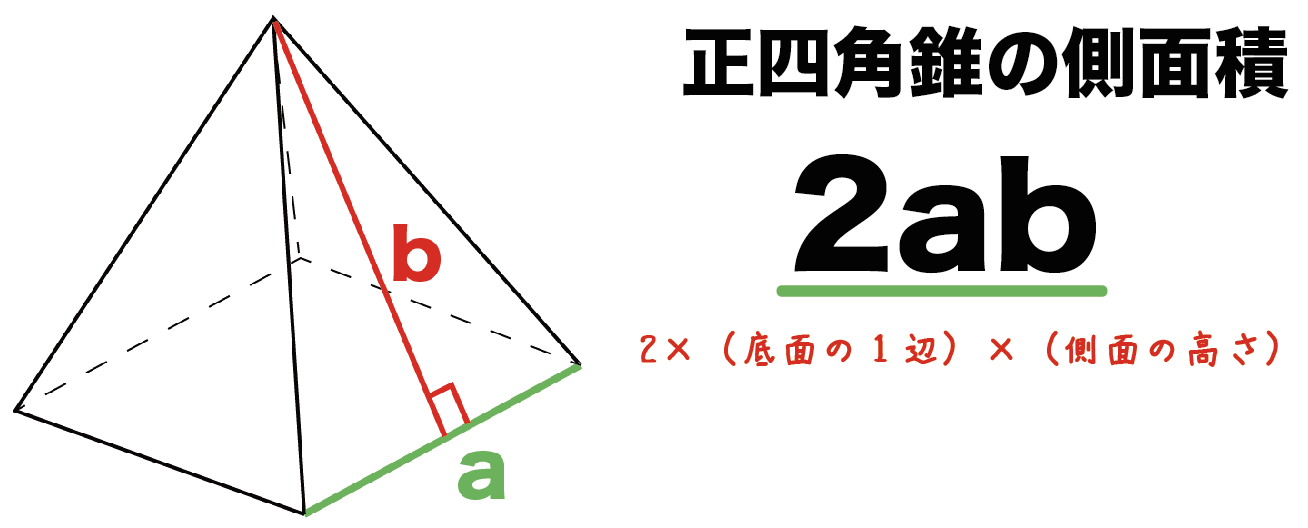


計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



角錐と円錐の体積 Youtube
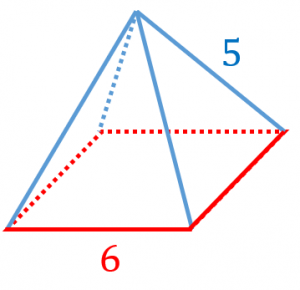


正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学



サクッとできればok 四角錐編 数学カフェjr


図は側面が正三角形の正四角錐である 一辺の長さは6 である 1 体積を求 Yahoo 知恵袋



0 件のコメント:
コメントを投稿