体積の意味 問題一括 (6,079Kb) 平行四辺形の面積(3) 三角形の面積(1) 三角形の面積(2) 三角形の面積(3) 三角形の面積(4)特に、三角形、平行四辺形、台形などの図形の面積問題が重要となってきます。 小学校6年生 で習う面積問題は、円の面積問題です。 単位を確認しよう 例)正方形の面積を表すとき単位が、 たてcm×よこcm=面積㎠ と表します。単位忘れは 減点の対象小学4年生の算数 台形・平行四辺形・ひし形・対角線 問題プリント 小学4年生の算数・台形・平行四辺形・ひし形・対角線の問題を繰り返し練習できるプリントです。
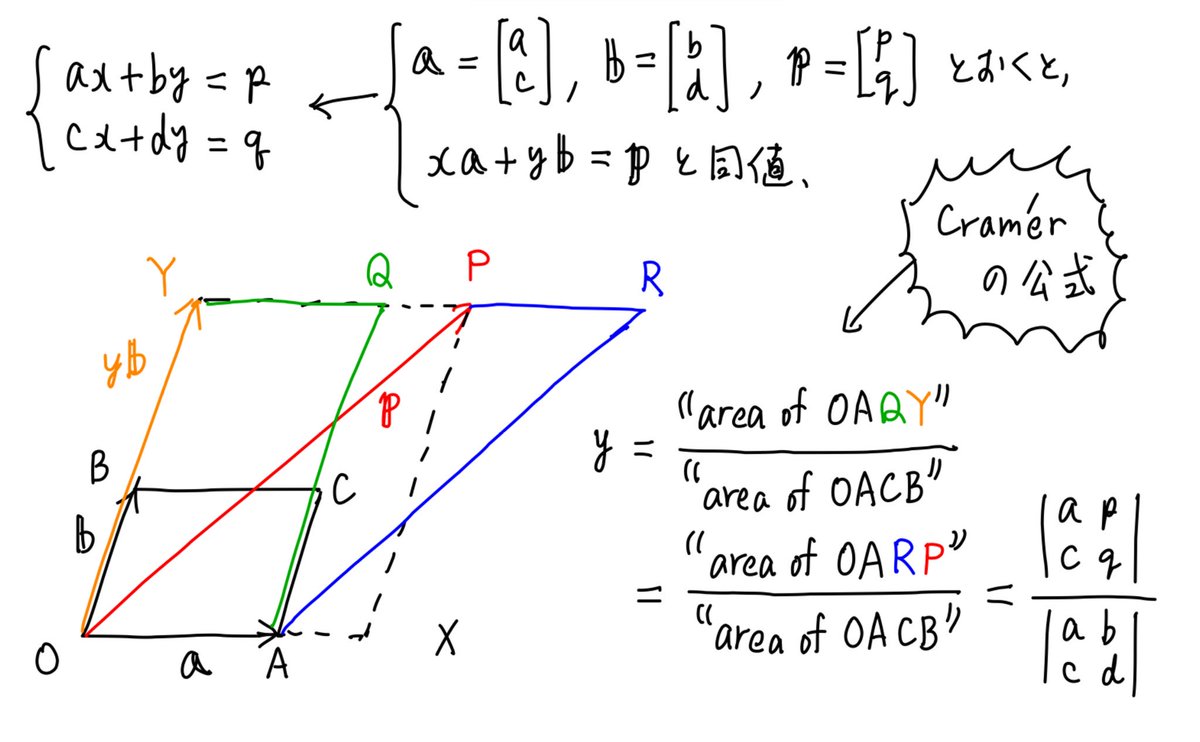
黒木玄 Gen Kuroki 数楽 行列式が体積 の 1倍 もしくは向き付けられた体積 だという事実も重要な数学的教養 高校でも問題練習のどこかで ベクトル A B と C D を2辺とする平行四辺形の面積が Ad になるという計算を含むものをやっているはず Ad
平行 四辺 形 体積
平行 四辺 形 体積-四角形 平行四辺形や三角形の面積 いろいろな四角形 平行四辺形先生問題 ひし形 ひし形変形 ひし形先生問題 四角形のかき方 平行四辺形のかき方 ひし形のかき方1 ひし形のかき方2 ひし形のかき方3 四角形の対角線1 対角線クイズ 四角形の対角線1中1の次回のテストは、おうぎ形の弧の長さ・面積、立体の表面積・体積の問題が出題されます。 この分野の基礎となるのは、小学校でやった図形の知識です。 三角形、台形、平行四辺形、円の面積を求められるかどうか。 ここが大切なんですね。


Www City Suwa Lg Jp Uploads Files Dc215ff8c23c9ddfad014eb749e Pdf
第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。< 平行六面体の体積> 2つのベクトルaとbの外積a×bは,aとb に垂直なベクトルであり,大きさはaとb の つくる平行四辺形の面積Sに等しい。又a×b の向きはaからbに,向かって回転するとき に,右ねじの進む方向である。従ってb × a はその反対向きであり以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。 ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。
小学校 5年生 量と測定 基礎的・基本的な問題 · 直方体・立方体の体積 · 体積の単位と測定 · 平均 · 単位量当たりの大きさ · 単位量当たりの大きさ(人口密度) · 平行四辺形や三角形の面積平行四辺形の面積公式は覚えない 自分で導き出せるようになろう 平行四辺形の面積の求め方 公式と計算例 モデルの体積を計算する 試行錯誤今回は、平行四辺形の面積の求め方について書いていきたいと思います。 平行四辺形の面積を求める公式 平行四辺形の面積を求める問題 問題① 《平行四辺形の面積の求め方》 問題② 《平行四辺形の面積の求め方》 問題③ 《平行四辺形の高さの求め方》 問題④ 《平行四辺形の底辺の求め方
三角形、平行四辺形の求積公式を導く際の順序と用いる方法 児童学部 児童学科 田村 壽 要旨:本論文は、小学校算数科における三角形と平行四辺形の求積の指導順序についての提案を示したものである。えば,長方形と平行四辺形について,平行四辺形 は長方形に変形できるという関係に着目し,平行 四辺形の面積を求める式を学習する。 本教材で扱う斜角柱の体積の求め方は,小学5 年生の平行四辺形の面積を求める学習を3次元に 拡張した内容である。右の平行四辺形で,辺bcを 底辺としたとき,その底辺に 垂直な直線ecなどの長さを 高さといいます。 また,辺abを底辺と したときの高さは,右の 図のようになります。 図1 東京書籍 新しい算数 5下,p35 この後,第5学年では三角形や台形など他の


Www City Suwa Lg Jp Uploads Files Dc215ff8c23c9ddfad014eb749e Pdf


Http Www Mathema Jp Wp Content Uploads 17 11 8f37d58b052c4ccea616c3f64a9249cb Pdf
体積の意味 問題一括 (6,079Kb) 平行四辺形の面積(3) 三角形の面積(1) 三角形の面積(2) 三角形の面積(3) 三角形の面積(4)第276問 長方形と平行四辺形 図形ドリル 6年生 平行四辺形 等積変形 長方形 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。N次元超球の体積はヤコビアン、曲面積は平行四辺形 上野孝司 16年7月4日 N次元超球体積はヤコビアン、曲面積は平行四辺形 1.Γ関数と極座標変換―N次元球の体積はヤコビアン 1‐1.3次元と4次元球の体積 半径r の3次元球の体積 4 3



高校入試 でる順ターゲット 中学数学100 四訂版 Amazon Com Books



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
平行四辺形の面積は dbcを2倍した値になるので24となります。 以上より rpqの面積を1としたとき、平行四辺形abcdの面積は24となるので 答えは24倍 となります。 ちょっと難しかったけど これも面積比を確実に見ていけば大丈夫な問題ですね! まとめ正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱平行四辺形(へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ平行である四角形のことである。 平行四辺形は、台形の一種である。 また、特殊な平行四辺形に長方形、菱形がある。



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ


Http Www Pref Okayama Jp Uploaded Attachment 1966 Pdf
今回は、平行四辺形の面積の求め方について書いていきたいと思います。 平行四辺形の面積を求める公式 平行四辺形の面積を求める問題 問題① 《平行四辺形の面積の求め方》 問題② 《平行四辺形の面積の求め方》 問題③ 《平行四辺形の高さの求め方》 問題④ 《平行四辺形の底辺の求め方平行四辺形の書き方なぜ? 上の章では、平行四辺形の書き方の手順について解説しました。 やり方としては、とっても簡単でしたね! だけど、なんでこんなやり方でできるの?と疑問に思った方もいるでしょう。平行四辺形の面積 まず, 2つのベクトル(ベクトルを横に書く悪習は辞めましょう) が張る平行四辺形の面積を考えよう 小学生でも習うこの公式 = (底辺) × (高さ) を思い出そう 底辺をとすると, これに対する高さは となる ここで, はとがなす角である すると, 面積は となる



ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張



三角比48 四面体の体積公式 怜悧玲瓏 高校数学を天空から俯瞰する
平行四辺形(へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ平行である四角形のことである。 平行四辺形は、台形の一種である。 また、特殊な平行四辺形に長方形、菱形がある。7・平行四辺形の面積 5年 平行四辺形って? まず、平行四辺形と言うのはどういう四角形なのか、おさらい。 2組の対辺(向かい合った辺)が平行な四角形を平行四辺形と言います。参考:「その13図形の性質と集合・四角形」。 そして、覚えておいてほしい名前など。下の図は一般的な平行四辺形です。 平行四辺形の面積はどのように求めればよいでしょうか? 既に分かっているかもしれませんが、ここでは なぜ、そうなるのか? というのも考えてみてください。 ヒントは「長方形」です。



数学の角度の問題 平行四辺形 中学数学に関する質問 勉強質問サイト


2
放物形 P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの平行四辺形の面積は dbcを2倍した値になるので24となります。 以上より rpqの面積を1としたとき、平行四辺形abcdの面積は24となるので 答えは24倍 となります。 ちょっと難しかったけど これも面積比を確実に見ていけば大丈夫な問題ですね! まとめ放物形 P11 平面図形の性質 P12 立体の体積(V),表面積(S)または側面積(F)および重心位置(G) P12 平均自乗誤差 P13 円板の最大応力(σmax)と最大たわみ(ωmax) P96 長柱の座屈 P97 各種断面形の軸のねじり P97 梁の公式 P98 キーの


Http Www Nagano C Ed Jp Iikita Entrance H28pdf H28hyokakanten Pdf


Www Edu City Yokohama Jp Sch Kenkyu Es Sansu Pdf H30 Jirei 3005jirei05 Pdf
第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。平行四辺形の面積素材集 今回の授業では、まだ公式までいかず、平行四辺形から長方形に形を変えることを理解させることに重点を置いて授業を進めていきました。 ご意見いただけたら幸いです。 5年算数「平行四辺形の面積」第2時 指導実践N次元超球の体積はヤコビアン、曲面積は平行四辺形 上野孝司 16年7月4日 N次元超球体積はヤコビアン、曲面積は平行四辺形 1.Γ関数と極座標変換―N次元球の体積はヤコビアン 1‐1.3次元と4次元球の体積 半径r の3次元球の体積 4 3



モデルの体積を計算する 試行錯誤



黒木玄 Gen Kuroki 数楽 行列式が体積 の 1倍 もしくは向き付けられた体積 だという事実も重要な数学的教養 高校でも問題練習のどこかで ベクトル A B と C D を2辺とする平行四辺形の面積が Ad になるという計算を含むものをやっているはず Ad
22 平行六面体の体積 空間ベクトル(3 次元ベクトル) a,b,c の作る平行六面体(下図) において, a ˆ b とc のなす角をθ とする a ˆ b はa,b の張る平面と直交するから, a,b の作る平行四辺形を底面と見たときの平行六面体の高さh は h " ∥c∥cosθ " ∥c∥¨ paˆbq¨c ∥aˆb∥∥c∥ paˆbq¨c四角形 平行四辺形や三角形の面積 いろいろな四角形 平行四辺形先生問題 ひし形 ひし形変形 ひし形先生問題 四角形のかき方 平行四辺形のかき方 ひし形のかき方1 ひし形のかき方2 ひし形のかき方3 四角形の対角線1 対角線クイズ 四角形の対角線1平行四辺形の書き方なぜ? 上の章では、平行四辺形の書き方の手順について解説しました。 やり方としては、とっても簡単でしたね! だけど、なんでこんなやり方でできるの?と疑問に思った方もいるでしょう。



高校数学b 平行六面体と空間ベクトルの演算 受験の月



ここが分かりませんやり方を教えてください Clear
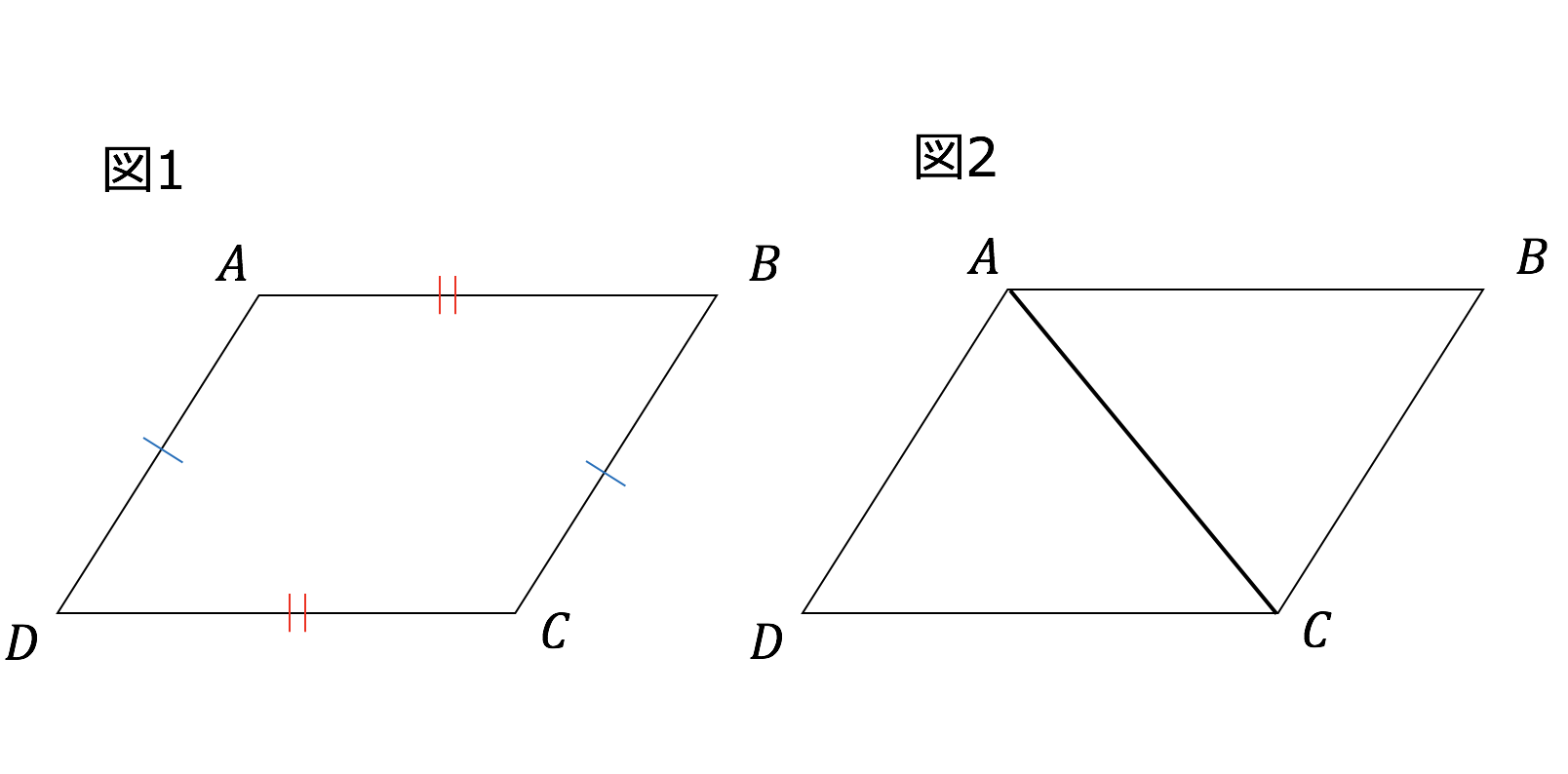
平行四辺形の条件 ある平面図形が平行四辺形であるための条件には、次の \(5\) つがあります。 このうちどれか \(1\) つでも条件を満たせば、その図形は平行四辺形と言えます。 条件①2 組の向かい合う辺が平行である これは平行四辺形の定義と同じ三角形は2つ合わせると 平行四辺形になります。 平行四辺形の半分だから 「÷2」です。 下底 上底と同じ 高さ 底辺 上底 高さ 台形も2つ合わせると 平行四辺形になります。 ひっくり返して横に並べ ると、もとの台形の2倍の 平行四辺形になります。



年の最高 図形 の 面積 無料の印刷物


Http Www Soumu Go Jp Programming Data 017 017 01 02 Pdf


2


14年慈恵医大4 京極一樹の数学塾


小5 面積の求め方を考えよう 平行四辺形 日本語版 Youtube


Http Himuka Miyazaki C Ed Jp Seisakuka Guidebook Betu3 Pdf


Http Www Edu Ctr Pref Nagano Lg Jp Kjouhou Manabi Hiroba 05 Review Mondai Mondai S Re Sho6 03 02 Pdf



体積比の問題です 中学数学に関する質問 勉強質問サイト



斜軸回転体の体積 応用編 傘型積分 おいしい数学



斜軸回転体の体積 応用編 傘型積分 おいしい数学



高校数学b ベクトルの外積 裏技 による法線ベクトル 空間の三角形の面積 平行六面体の体積 四面体の体積 受験の月


Core Ac Uk Download Pdf Pdf


図形問題が驚くほど得意になる基本問題とは あおぞら塾


Www City Mihara Hiroshima Jp Uploaded Life 540 Misc Pdf
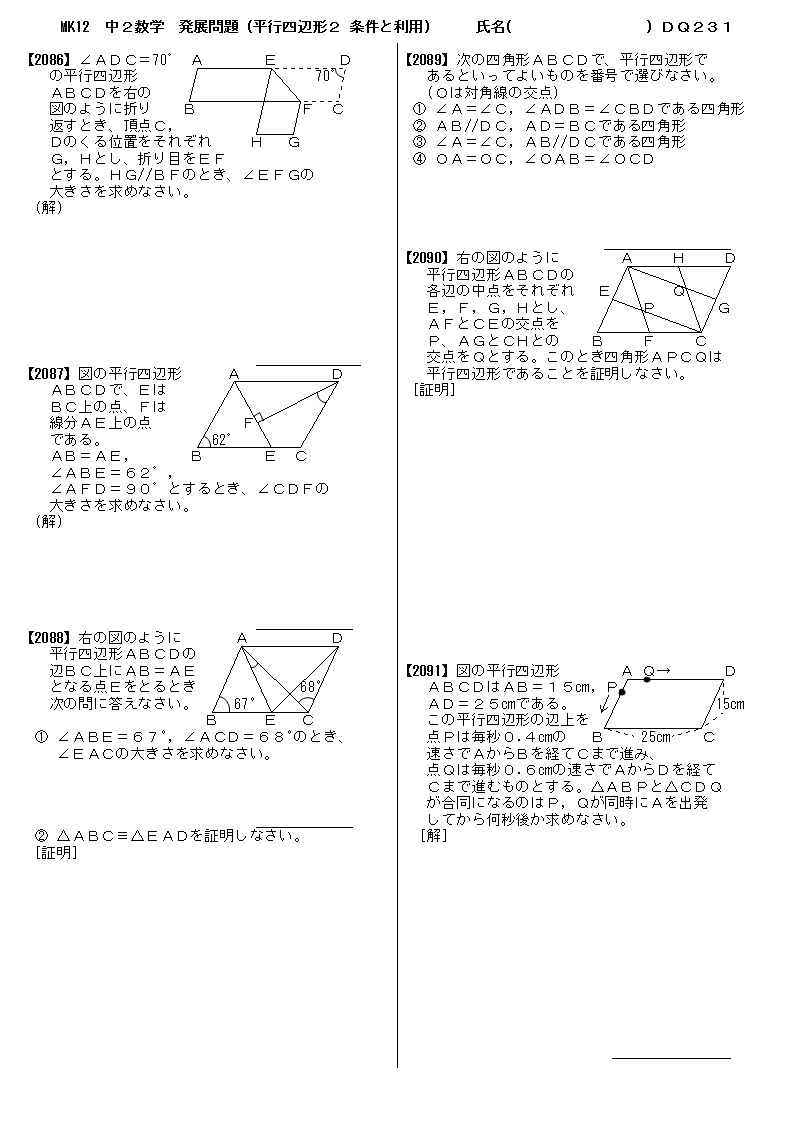


無料 中2数学 応用 発展問題 問題プリント 331 図形の相似6 面積比 体積比



5年 直方体と立方体の体積 算数イメージ動画集 大日本図書


2


Www Ishikawa C Ed Jp Content Tashikana 07jirei 07j21 07j21b1 Pdf


2
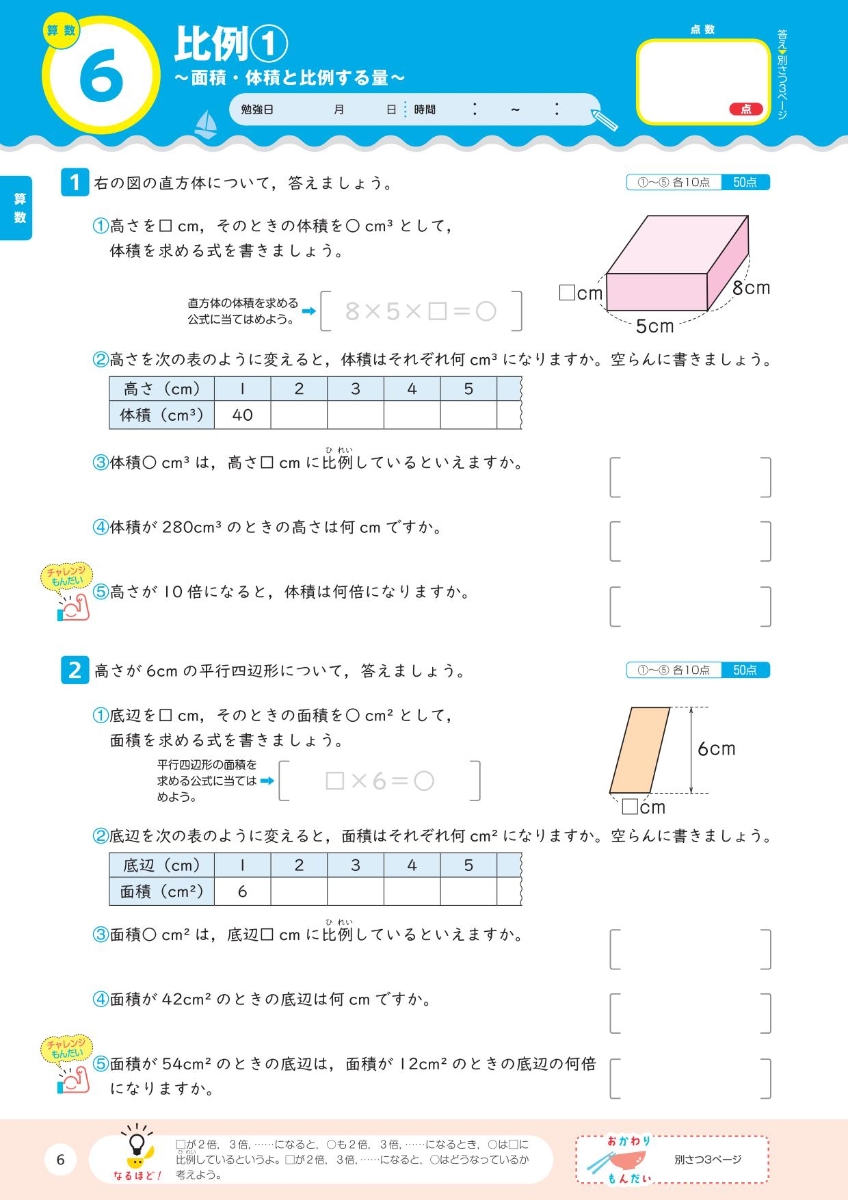


楽天ブックス 大盛り 夏休みドリル 小学5年生 旺文社 本



ここが分かりませんやり方を教えてください Clear


2



メルカリ 小6算数 角柱と円柱の体積 問題48ページ分 スモールステップで学力アップ 参考書 444 中古や未使用のフリマ



モデルの体積を計算する 試行錯誤


2


3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
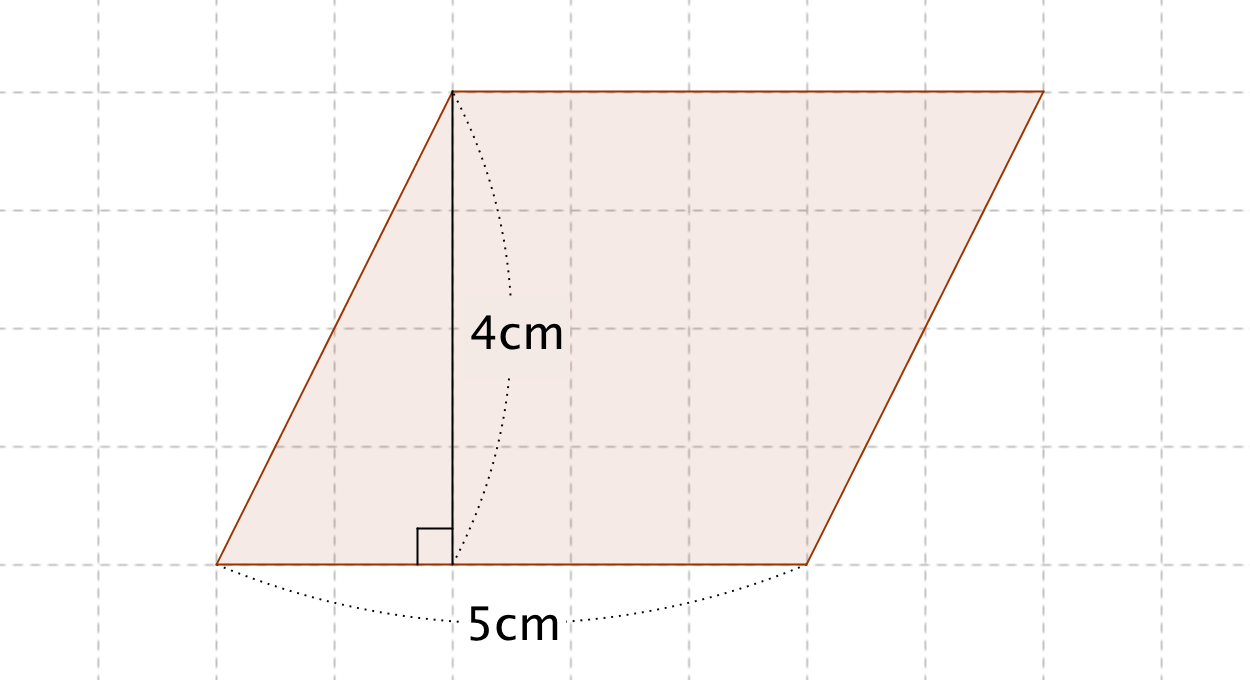


平行四辺形の面積の公式 算数の公式



小5 算数 小5 41 平行四辺形の面積 Youtube


Http Goose Math Akita U Ac Jp Mikami Hokou2 2 Nup Pdf



中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル


Http Www1 Center Spec Ed Jp Action Common Download Main Upload Id


Www Gakuto Co Jp Docs Ps Sansu Pdf Nenoshi27 5n B All Pdf
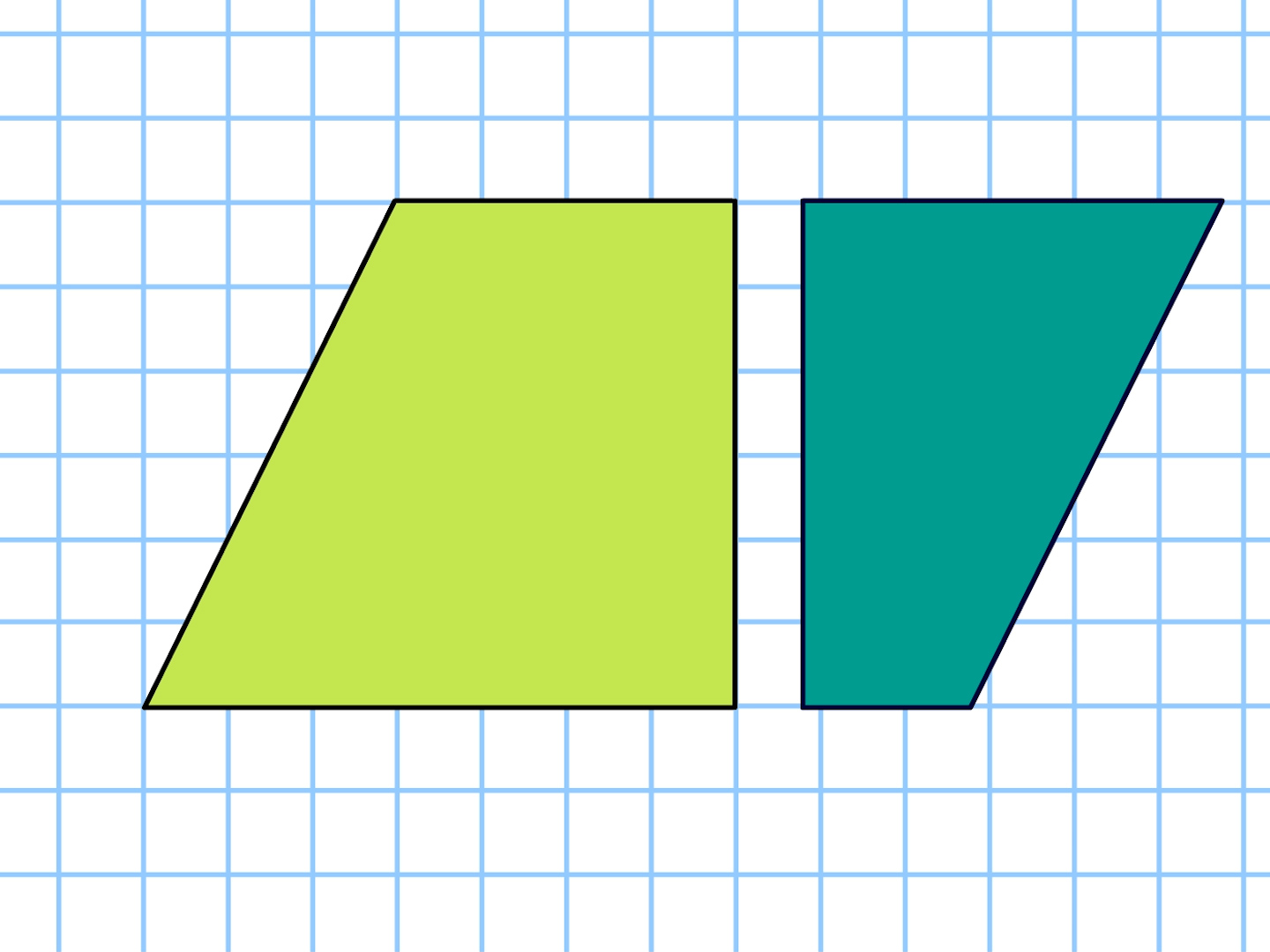


5年 平行四辺形の面積 算数イメージ動画集 大日本図書


Http Shws Cc Oita U Ac Jp Shibata M2 Download Emathii Practice2ans Pdf


重積分の変数変換とヤコビアン リーマン空間における多重積分


My Math Note


Fdkyb3b9c093sr81e Com 99 Af Ab E8 A3 E6 9e 90 E7 Ba E9 96 93 E5 9b E5 81 Ae E9 9d E7 8d 81 A8 E4 93 E7 8d



0 Jpg


Www Kyokyo U Ac Jp Kyoumu Jicci E Sansuu18 Pdf


Gakuto Co Jp Docs Download Pdf H28 3 14 Pdf



娘ちゃんの宿題 美樹のブログ


Http Menet Ed Jp Kaihigashi Es Information Action Common Download Main Upload Id 1755


Http Www Ocw Titech Ac Jp Index Php Module General Action Download File 0 45 Pdf Type Cal Jwc


齊藤数学教室のお弟子さんを取ります 年令実力は問わず



4 の 問6の 2 それぞれ 解き方を教えてください Clear



四角柱の表面積 数学 Okwave



この2問の問題の解き方教えていただきたいです Clear
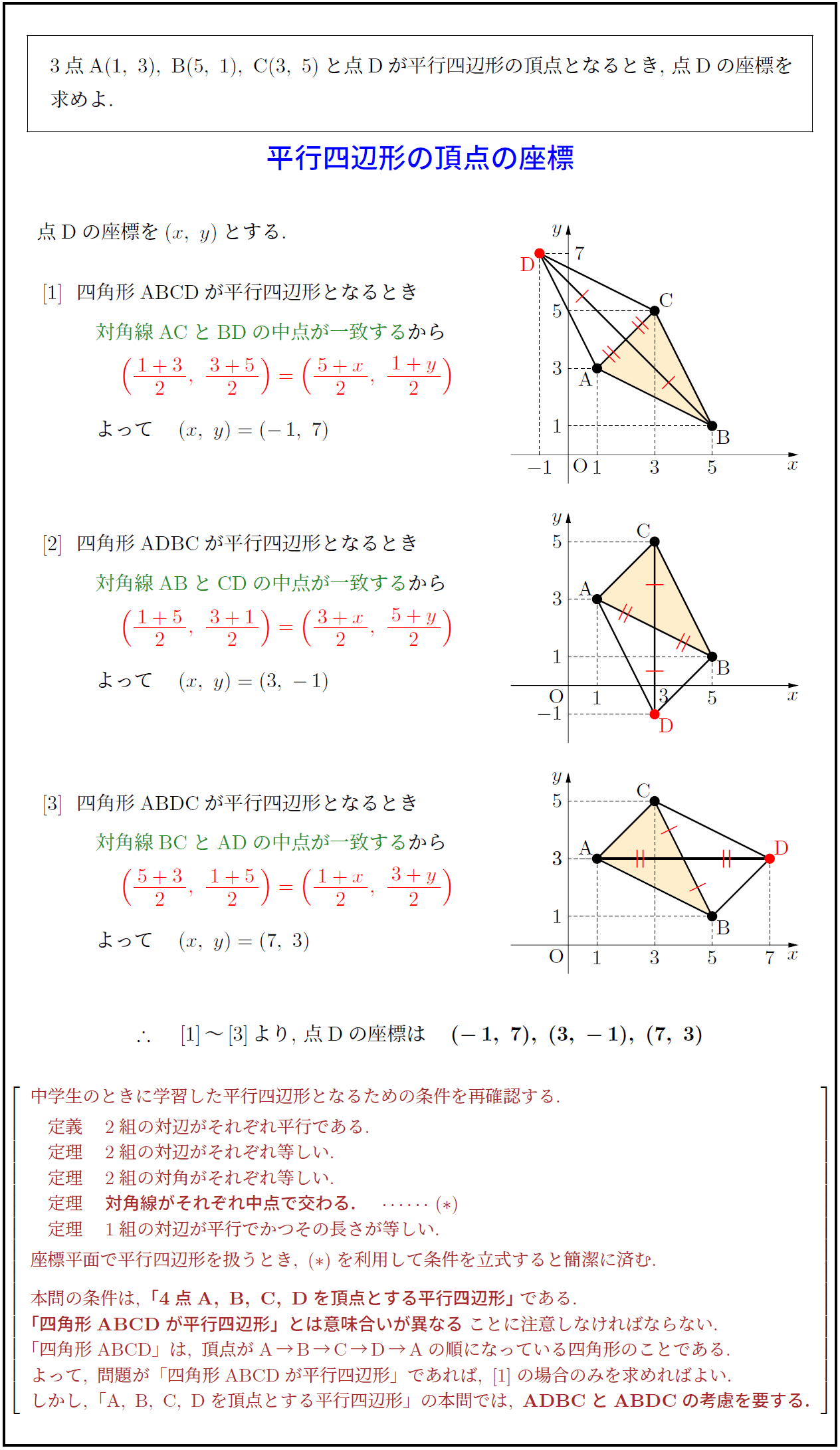


高校数学 平行四辺形の頂点の座標 受験の月


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf



簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく



この問題の答えにeprqは平行四辺形とかかれていて その理由がわかりません 教えて下 Clear
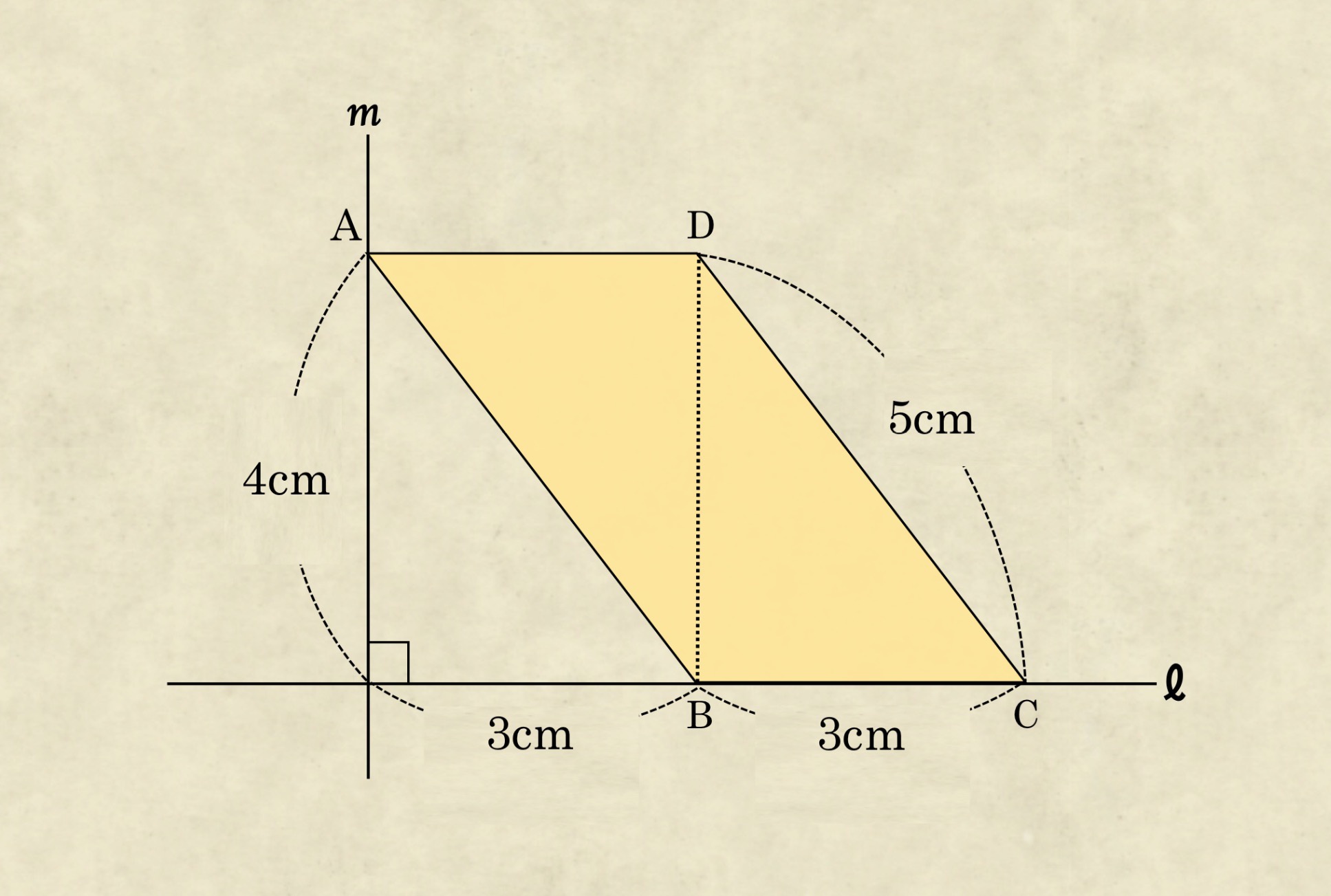


17年2月号の巻 難攻不落の算数城攻略 忍者エピス丸 Epis Education Centre Epis Education Centre



ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門


Fdkyb3b9c093sr81e Com 99 Af Ab E8 A3 E6 9e 90 E7 Ba E9 96 93 E5 9b E5 81 Ae E9 9d E7 8d 81 A8 E4 93 E7 8d



メルカリ 026 小学生算数 面積 体積の公式 暗記シート 中学受験 参考書 700 中古や未使用のフリマ



ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門


2



最速 年センター試験解説 福田の入試問題解説 年センター試験iib第4問 空間ベクトルと四面体の体積 Youtube


Http School City Tajimi Lg Jp Kyoiku Wp Content Uploads 15 03 62c9790f4bdc505e278cd45e8cc Pdf


Core Ac Uk Download Pdf Pdf



外積を使って解く入試問題例 東大落ちの受験勉強法


Http Jac Web Com Wp Content Uploads Elephan Pdf


2


分数のかけ算 面積や体積を求める On Vimeo


Www Town Osakikamijima Hiroshima Jp Material Files Group 13 Sansu4 Pdf



数学カフェjr


2



ベクトルの図形への応用 高校数学に関する質問 勉強質問サイト



ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張


Qsj1984 Com Wp Content Uploads 04 2c7774ac5ba2a91d70a755da5b393c Pdf



数学の証明問題 中学数学に関する質問 勉強質問サイト



斜軸回転体の体積 応用編 傘型積分 おいしい数学


回転体 パップスギュルダンの定理 新河岸 川越 の学習塾next Stage 自分に負けるな



積分 いわゆる傘型分割 Okwave


Http Www Saiensu Co Jp Book Support 978 4 003 6 Parallelepiped Pdf



面積 体積説明器等 有限会社 コバック 岐阜県高山市


Http Staff Miyakyo U Ac Jp H Uri Blog Archive Lecture Senkeidaisu 03 Volume Pdf


相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



平行四辺形の対角線の求め方を教えてください 高校数学に関する質問 勉強質問サイト


3次元面積分と体積積分


Http Www2 Meijo U Ac Jp Yonishi Teaching Meijo Eng Calculus2 Parallelogram Pdf
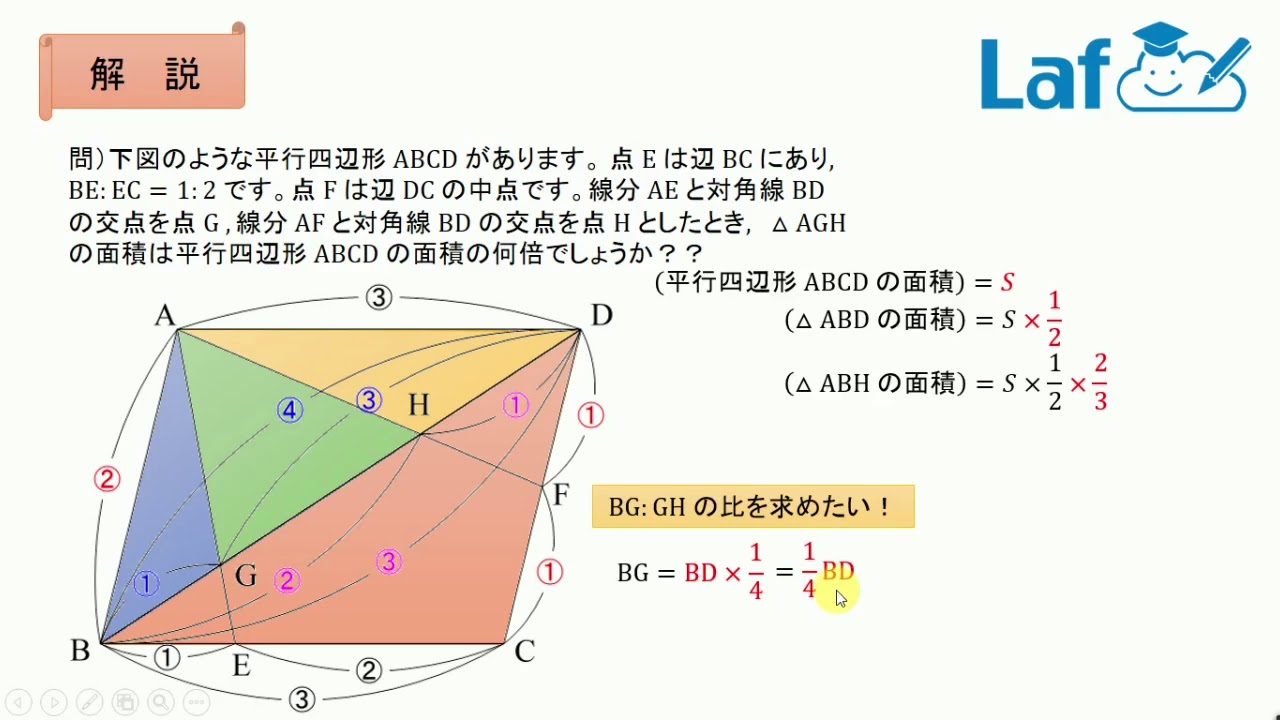


中3数学 相似な図形 三角形の面積は平行四辺形の面積の何倍 Youtube



外積を使って解く入試問題例 東大落ちの受験勉強法


2



0 件のコメント:
コメントを投稿